How many Mega-Pixel are Necessary in Digital Photography?

The optimum size of a digital image in mega-pixel

Author:D.Thaler Created:Feb 2014 Last changed:2014-03-17

Summary

Modern digital photo cameras still compete in ever higher resolutions and therefore output images of ever increasing pixel size. Full Frame Digital SLR now (2014) stop at about 36 Mpx [1] (e.g. Nikon D800). But how many million image pixels are actually useful?

• The visual acuity of humans varies between 0.5 arc-minutes angular resolution for younger people up to 1.0 and more for older people. [2]
• Consider a photo print. This print can be reasonably watched as a whole (without pixel peeping) from a distance not closer than the image diagonal, more comfortable even more distant.

Both statements imply a certain optimum image resolution [1] measured in mega-pixel.

Detailed calculation gives following result for \(M\) in mega-pixel (valid only for distances longer than one image diagonal because of a simplifying approximation; see Calculation):

\[M(\epsilon,k) = N_{\mathrm{Nyquist}} \cdot \frac{4}{\epsilon^2}\arctan^2\left(\frac{1}{2k}\right)(a^2 + 2 + a^{-2})^{-1/2}\]

Let \(\epsilon\) be the angle (in radiant) that can be resolved by human eyes (visual acuity), \(k\) be the multiples of the image diagonal as a measure for the watching-distance and \(a=\frac{x}{y}\) be the aspect ratio of the image (width divided by height), and \(N_{\mathrm{Nyquist}}=2\;..\;4\) the necessary factor for increasing the pixel-number because of the Nyquist-Shannon theorem [3].

The result can be displayed as graph for different values of acuity:

Optimum image size in pixel as a function of watching-distance for double (left) and quadruple (right) pixel density. The true value for \(N_{\mathrm{Nyquist}}\) is somewhere in between. An aspect ratio of the image of \(a=3:2\) and visual acuity from \(\epsilon=0.5'\) to \(\epsilon=1.5'\) are presumed.

Depending on the visual acuity there are optimum resolutions reaching from

• estimated 60 Mpx for very sharp eyes (acuity of 0.5’) and a close watching distance of about the image diagonal or even closer
• about 14 Mpx for good eyes (0.75’) and a moderate watching distance of 1.5 times the image-diagonal
• less than 6 Mpx for standard eyes** (1.0’) and a comfortable watching distance of 1.5 to 2 times the image-diagonal.

Note

6 to 10 mega-pixel is a sufficient image resolution for photo prints watched in standard situations. - Virtually all computer screens cannot meet even this moderate condition.

Very high end performance has room for improvements up to about 60-80 Mpx, provided there is no blur due to diffraction because of small apertures and other optical restrictions. [4] [5]

Footnotes and References

[1]	(1, 2) The number of effective sensor pixels or image pixels differs from the nominal number of sensor pixels due to a variety of reasons and is usually significantly lower. Compare: Understanding Digital Camera Resolution

[2]	Welche Sehschärfe ist normal?

[3]	(1, 2) en.wikipedia.org/wiki/Nyquist-Shannon_sampling_theorem

[4]	http://en.wikipedia.org/wiki/Depth_of_field#Diffraction_and_DOF .

[5]	http://www.cambridgeincolour.com/tutorials/diffraction-photography.htm

Calculation

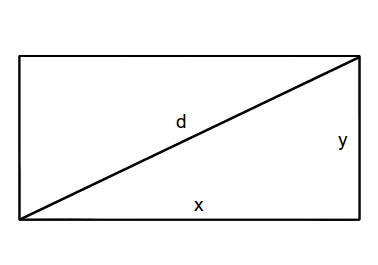
Given an image with the relative size width x height (\(x \cdot y\)) the diagonal is \(d=\sqrt{x^2+y^2}\).

With Pythagoras and the relation for the aspect ratio \(a=x/y\) the image diagonal can be written as \(d^2 = x^2 + y^2 = x^2 + x^2/a^2 = x^2\left(1+\frac{1}{a^2}\right)\)

leading to

(1)\[\frac{x}{d} = \sqrt{\frac{1}{1+\frac{1}{a^2}}} .\]

A similar calculation \(d^2 = x^2 + y^2 = y^2 + y^2 a^2 = y^2\left(1+{a^2}\right)\)

yields

(2)\[\frac{y}{d} = \sqrt{\frac{1}{1+a^2}} .\]

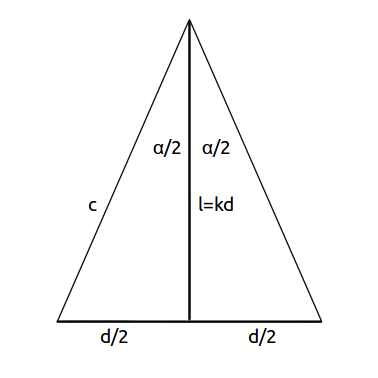
Generally the image-diagonal \(d\) is watched from a distance \(l=kd\) (with \(k\) as a multiple of the diagonal \(d\)) with the angle \(\alpha\).

With the trigonometrical relation

\[\tan (\alpha/2) = \frac{d/2}{l} = \frac{1}{2k}\]

a relation for the watching angle \(\alpha\) can be derived:

(3)\[\alpha = 2 \arctan\left(\frac{1}{2k}\right) .\]

With the visual acuity \(\epsilon\) the number of pixels that can be resolved along the diagonal is approxymately

(4)\[N_d \approx \frac{\alpha}{\epsilon}\]

provided the distance is not too small so that (see figure above) roughly \(c \approx l\) is valid. Anyway the approximation poses a more severe condition on pixel resolution than the exact calculation. The exact solution would take into account that the resolved pixel size at the image edges is coarser than at the center.

With the help of (1) and (2) and using the similarity \(N_x = N_d \cdot x/d,\;\mathrm{etc...}\) one gets for the image resolution in pixel

\[M_0 = N_x \cdot N_y = N_d \left[\left(1+a^2\right)\left(1+1/a^2\right) \right]^{-\frac{1}{2}}\]

Further refinement yields

(5)\[M(\epsilon,k) = \frac{4}{\epsilon^2}\arctan^2\left(\frac{1}{2k}\right)(a^2 + 2 + a^{-2})^{-1/2}\]

One might expect equation (5) is the final result. But to resolve a pixel pattern like “0,1,0,1,0,1,0” in one dimension at least a doubled sampling rate is necessary because one cannot rely that the samples exactly fit the patterns. If the sample falls in between, the result will be series like “0.5,0.5,0.5,0.5,0.5,0.5,0.5” and so no structure is resolved. Mathematically this is due to the so called Nyquist-Shannon-Theorem [3]

The factor 2 is true for 1-dimensional data f(x). Having 2-dimensional data f(x,y) one might expect the square \(2^2=4\). This is not necessarily true. Most structures in 2-D images are rather lines and filaments than “pepper and salt”-structures and together with sophisticated 2-D sensor grid designs this is likely to reduce the factor.

So let us call the factor necessary to for correct sampling the Nyquist-factor \(N_{\mathrm{Nyquist}}\) and give it a value somewhere between 2 and 4. Thus the final result shown to us:

---

(6)\[M(\epsilon,k) = N_{\mathrm{Nyquist}} \cdot \frac{4}{\epsilon^2}\arctan^2\left(\frac{1}{2k}\right)(a^2 + 2 + a^{-2})^{-1/2}\]

---

Note

Any comments to info at foehnwall dot at