About the Atmosphere in a Rotating Cylinder

Author:D.Thaler Created:Feb 2013 Last changed:2018-06-23

Some rudimentary hydrostatics and dynamics

Motivation

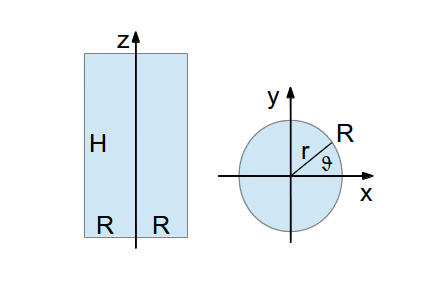
Sketch of a (rotating) Cylinder

Left: front view (with height \(H=50\;km\) and radius \(R=8\;km\)); Right: top view (with Radius R); x,y,z are the cartesian coordinates; r, \(\vartheta\), z the cylindrical coordinates

In the science fiction novel “Rendezvous with Rama” by A.C. Clarke a huge space craft (Rama) in the shape a rotating hollow cylinder with the inner height of 50 km and the radius of about 8 km filled with air and rotating with a period of 4 Minutes is the main location of the novel. In the novel some properties of the Rama atmosphere are depicted. The following fragmentary work investigates whether and how the novel-atmosphere conflicts with atmospheric physics.

Dimensions of Rama
Height (Lenght resp.)	\(H=\) 50 km = 50 000 m
Radius	\(R=\) 8 km = 8000 m
Period of rotation	\(\tau=\) 4 min = 240 s
Angular velocity	\(\omega=2\pi/\tau = 0.0262 s^{-1}\)

Basics

Consider a hollow cylinder in space with the inner height H and the radius R constantly rotating along the central axis with the period \(\tau\) and filled with air with similar mixing ratios as in the earth atmosphere. With \(\omega = 2\pi/\tau\) the equation of motion in a rotating framework (without gravitation) in coordinate system independent form reads (e.g. Holton 2004):

\[\frac{d\mathbf{v}}{dt} = {-2 \boldsymbol{\omega} \times \mathbf{v} - \boldsymbol{\omega} \times \boldsymbol{\omega} \times \boldsymbol{r} - \frac{1}{\rho}\nabla p - \mathbf{F_{fr}}.}\]

\(\mathbf{v}\) is the 3-dimensional velocity vector, \(\boldsymbol{\omega}\) is the 3-dimensional angular velocity vector in the direction of rotation, \(\boldsymbol r\) is the position vector, \(p\) the air pressure and \(\rho\) the air density.

The term at the left hand side is the individual change of velocity of an air parcel, the first term at the right hand side is the Coriolis force per unit mass, the second the outward directed centrifugal force, the third the pressure gradient, and \(\mathbf{F_{fr}}\) the unspecified friction term.

Equations of motion in cylindrical coordinates

With the help of the transformation relations for cylindrical coordinates (Holton, 2004, Appendix C.3.b) the above equation of motion is (neglecting friction):

• \(r\) - component (radial component directed away from the axis of rotation):

\[\frac{\partial v_r}{\partial t} + v_r \frac{\partial v_r}{\partial r} + \frac{v_\vartheta}{r} \frac{\partial v_r}{\partial \vartheta} + w \frac{\partial v_r}{\partial z} - \frac{v_\vartheta^2}{r} = - \frac{1}{\rho}\frac{\partial p}{\partial r} + 2 \omega v_\vartheta + \omega^2 r\]

• \(\vartheta\) - component (tangential component):

\[\frac{\partial v_\vartheta}{\partial t} + v_r \frac{\partial v_\vartheta}{\partial r} + \frac{v_\vartheta}{r} \frac{\partial v_\vartheta}{\partial \vartheta} + v_z \frac{\partial v_\vartheta}{\partial z} + \frac{v_r v_\vartheta}{r} = - \frac{1}{\rho}\frac{1}{r}\frac{\partial p}{\partial \vartheta} - 2 \omega v_r\]

• \(z\) - component (along the axis of rotation):

\[\frac{\partial v_z}{\partial t} + v_r \frac{\partial v_z}{\partial r} + \frac{v_\vartheta}{r} \frac{\partial v_z}{\partial \vartheta} + v_z \frac{\partial v_z}{\partial z} = - \frac{1}{\rho}\frac{\partial p}{\partial z}\]

Coriolis force

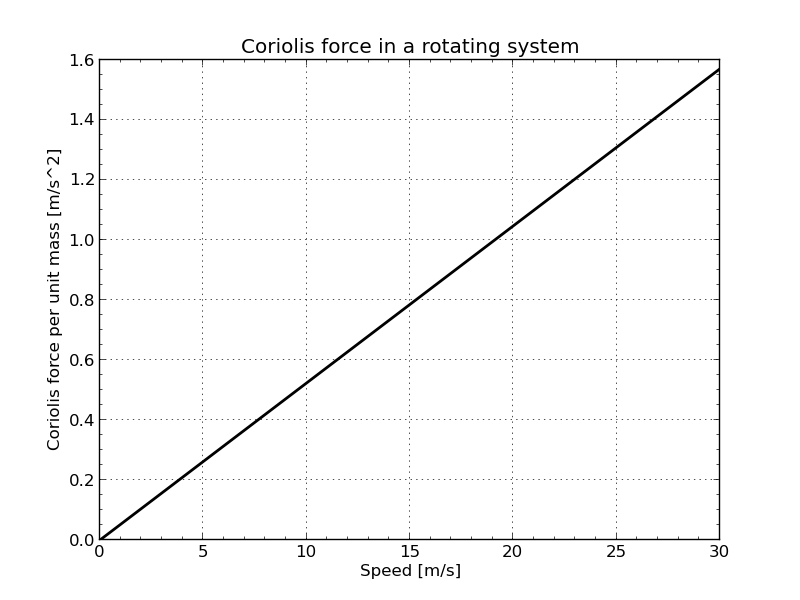
For velocities perpendicular to the axis of rotation the absolute value of the Coriolis force per unit mass is

\[|F_c|=|2\omega\,v_{\bot}|\ .\]

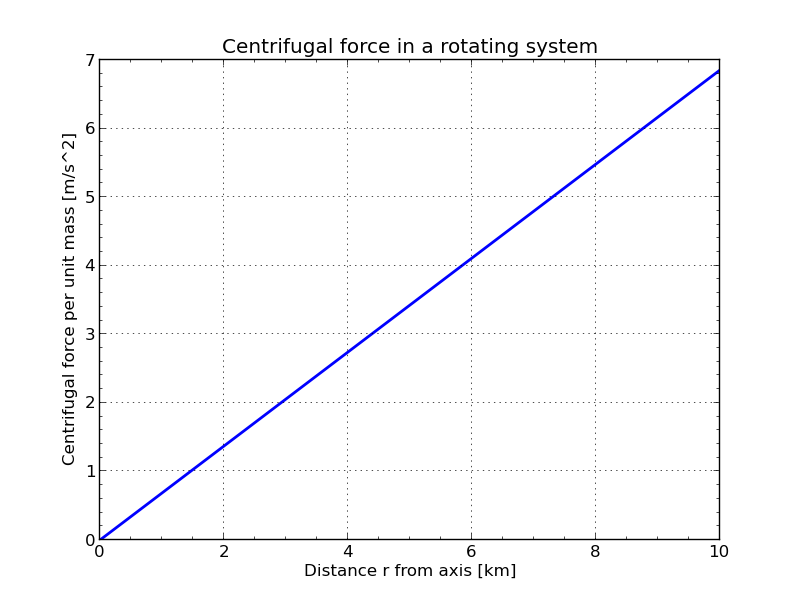
For the angular velocity \(\omega = 2\pi/(240\ \textrm{s})\) the graphic below gives some estimates for the magnitude of the forces involved.

Especially for radial directions with increasing speed it has a big influence on motions.

Centrifugal force

The centrifugal force acts in the rotation frame in outward radial direction with the value

\[F_z = \omega^2\, r\ .\]

It acts in this case as a sort of artificial gravitation. Starting from zero at the axis of rotation it is increasing to values of about 55% of standard earth gravitation.

Barometric Equation

Considering an atmosphere in rest all terms with velocity \(\mathbf{v}\) vanish and only the radial components perpendicular to the axis of rotation remain. So the remaining hydrostatic equation in cylindrical coordinates r in radial direction reads:

\[0 = {+\, \omega^2 r - \frac{1}{\rho}\frac{\partial p}{\partial r} .}\]

The (apparent) centrifugal force is balanced by the pressure gradient force. Inserting the ideal gas equation for air \(\rho=p/(R_L T)\) with Temperature \(T\) and with the gas constant for (dry) air \(R_L\approx 287\, \textrm{J/(kg K)}\) we get:

\[\frac{1}{p}\frac{\partial p}{\partial r}=\frac{\omega^2 r}{R_L T}.\]

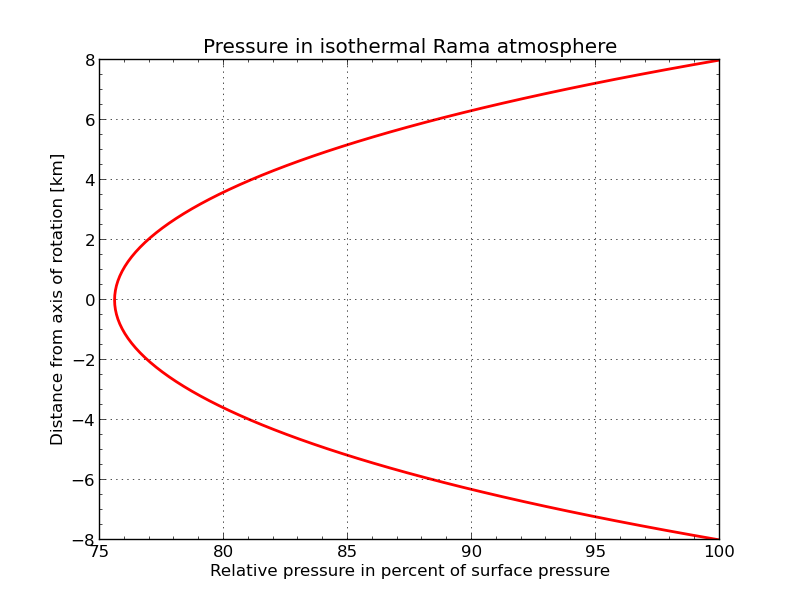
Integration from \((r=0,\,p_0)\) to \((r,\, p)\) and taking Temperature now as a constant \(T_0\) one yields

\[\frac{p(r)}{p_0}=\exp\left(\frac{1}{2} \frac{\omega^2 r^2}{R_L T_0}\right) .\]

Inserting

\[\omega = 2\pi/(4 \cdot 60)\, \textrm{s}^{-1})\approx 0.0262\, \textrm{s}^{-1}\ \textrm{and}\ R=8000\,\textrm{m}\]

the ratio between the higher air pressure at at the inner cylinder surface and the lower one at the axis at constant temperature of about zero centigrade \(T_0\approx 273\,\textrm{K}\) is about \(\frac{p_0}{p_0(R)} \approx 76\ \%\) .

In “Rendezvous with Rama” A.C. Clarke depicts a situation where humans initially cannot breath near the axis of rotation and feel very comfortable at the “bottom” of the cylinder. To circumvent this inconvenience later on the author introduces an increase of oxygen concentration. The above calculations clearly show that there is a flaw in Clarke’s assumptions. Presuming there is a pressure close to terrestrial sea level values at the cylinder surface there would be a still quite comfortable pressure at the axis of about terrestrial 2500 m mean sea-level values.

Adiabatic Temperature Gradient

The Potential Temperature for an ideal gas reads:

\[\Theta = T \left ( \frac{p_{00}}{p} \right )^{R_L/c_p},\]

with \(c_p \approx 1004\;J/(kgK)\), the specific heat of dry air at constant pressure and \(p_{00}\), a constant reference pressure, usually 1000 hPa.

By definition adiabtic means constant potential temperature \(d\Theta = 0\). Logarithmic differentiation along the radial coordinate \(r\;\) thus gives for an adiabatically stratified atmosphere:

\[\frac{1}{\Theta}\frac{\partial \Theta}{\partial r} = \frac{1}{T} \frac{\partial T}{\partial r} - \frac{R_L}{c_p}\frac{1}{p}\frac{\partial p}{\partial r} = 0 .\]

Thus the adiabatic radial temperature gradient with the help of the ideal gas equation yields the very general form:

\[\frac{1}{T}\frac{\partial T}{\partial r} = \frac{R_L}{c_p} \frac{1}{p} \frac{\partial p}{\partial r}\]

Because of the hydrostatic relation for a rotating atmosphere contained in a cylinder (without gravitation)

\[\frac{1}{p} \frac{\partial p}{\partial r} = \frac{\omega^2 r}{R_L T}\]

(with \(T = T(r)\;\)) one yields

\[\frac{\partial T}{\partial r} = \frac{\omega^2 r}{c_p} .\]

Integrated in the limits between 0 and r with \(T(0)=T_0\) and \(T(r)=T\) makes

\[T(r) = T(0) + \frac{1}{2} \frac{\omega^2 r^2}{c_p} .\]

Inserting appropriate values for \(\omega\), \(c_p\) and \(T(0)=273.15\;K\) gives as a result for \(T(r)\) the image below.

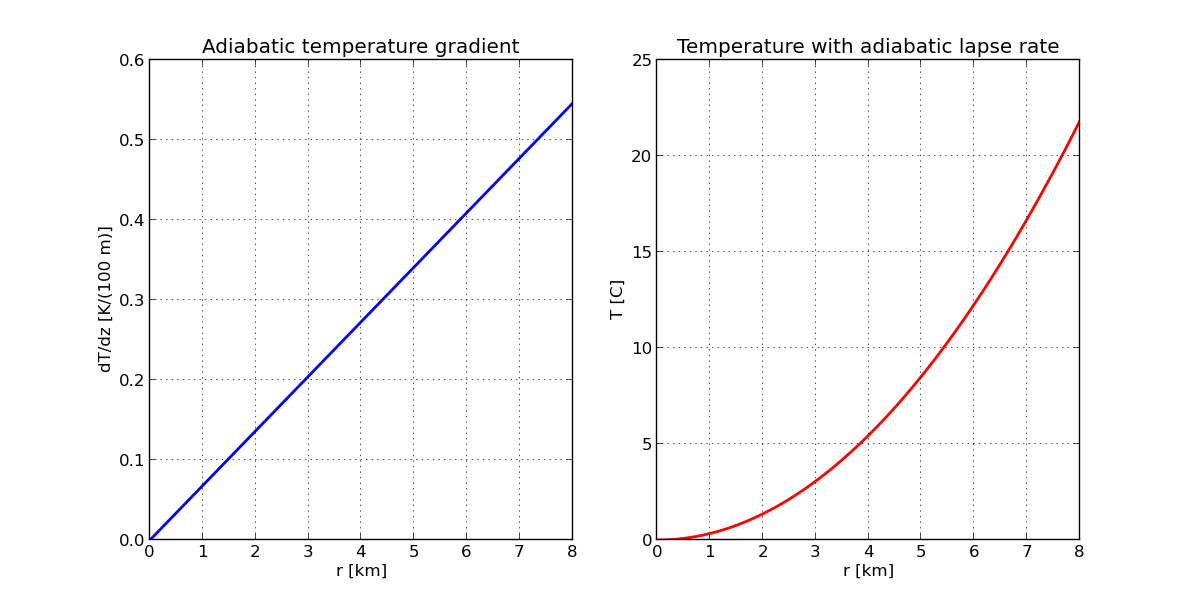
Adiabatic temperature gradient (left) and adiabatic temperature stratification (right) a Rama-atmosphere.

Compared with the vertically constant terrestrial adiabatic temperature gradient of 0.98 K/100 m one can see:

• the Rama gradient is “height”-dependent and vanishes at the axis (because of the vanishing centrifugal force)
• the adiabatic temperature profile is curved and not linear
• the adiabatic temperature gardient is always lower than the terrestrial atmosphereic values suggesting a lower overall vertical stability concerning thermal convection

---

To be continued …

… with some investigations about simple stationary flow regimes

References

• Clarke, Arthur C. (1973?): Rendezvous with Rama.
• Holton, James R. (2004): An introduction to dynamic meteorology. 4th edition. Elsevier Academic Press

Any comments to info at foehnwall dot at